
Мазмұны:
- 1 -қадам: Монохроматты жарықдиодтан шығатын жарықты түсіну
- 2 -қадам: Параболамен таныстыру
- 3 -қадам: Гаусс қисығына кіріспе
- 4 -қадам: Геогебра көмегімен демонстрация
- 5 -қадам: Светодиоды бар нақты өмір мысалы: ағын шыңы мен қабаттасатын ағындарды есептеу
- 6 -қадам: Эксперименталды лампаның монохроматикалық жарық диодтарын зерттеу енді аяқталды
- Автор John Day day@howwhatproduce.com.
- Public 2024-01-30 10:23.
- Соңғы өзгертілген 2025-01-23 14:50.



Барлық жасаушыларға және инструктивті қауымдастыққа сәлем.
Бұл жолы Merenel Research сізге таза зерттеу мәселесін және оны математикамен шешу әдісін ұсынады.
Мен өзім жасаған RGB жарықдиодты шамының жарық ағындарын есептегенде менде бұл мәселе болды (мен оны қалай құруды үйретемін). Интернетте кеңінен қарағаннан кейін мен жауап таба алмадым, сондықтан мен мұнда шешімді орналастырамын.
МӘСЕЛЕСІ
Физикада көбінесе Гаусс таралуының формасы бар қисықтармен күресуге тура келеді. Иә! Бұл ықтималдықты есептеу үшін қолданылатын қоңырау тәрізді қисық және бізге ұлы математик Гаусс әкелді.
Гаусс қисығы нақты физикалық қосымшаларда кеңінен қолданылады, әсіресе, егер біз көзден таралатын немесе қабылдағыштан алынған сәулемен күресуге мәжбүр болсақ:
- радио сигналының шығуы (мысалы, Wi-Fi);
- светодиодтан шығатын жарық ағыны;
- фотодиодты оқу.
Өндірушінің деректер кестесінде бізге Гаусс ауданының нақты мәні беріледі, бұл спектрдің белгілі бір бөлігіндегі жалпы сәулелену қуаты немесе жарық ағыны болады (мысалы, жарық диодты), бірақ нақты сәулеленуді есептеу қиынға соғады. қисық шыңында шығарылады немесе екі жақын көздің сәулеленуін білу одан да қиын, мысалы, егер біз жарық диодты шамнан артық жарықтандыратын болсақ (мысалы, көк және жасыл).
Бұл нұсқаулықта мен сізге Гауссты қисық жолмен қалай жақындату керектігін түсіндіремін: парабола. Мен сұраққа жауап беремін: Параболада қанша Гаусс қисықтары бар?
SPOILER → ЖАУАП:
Гаусс аймағы әрқашан 1 бірлік.
Табаны мен биіктігі бірдей сәйкес параболаның ауданы салыстырмалы Гаусс ауданынан 2,13 есе үлкен (графикалық демонстрация үшін суретті қараңыз).
Гаусс параболасының 46,94% құрайды және бұл қатынас әрқашан дұрыс.
Бұл екі сан 0.46948 = 1/2.13 осылайша байланысты, бұл Гаусс қисығы мен оның параболасы арасындағы қатаң математикалық байланыс және керісінше.
Бұл нұсқаулықта мен сізді біртіндеп ашуға апарамын.
Бізге қажет жалғыз құрал - бұл Geogebra.org, диаграммаларды құрудың тамаша онлайн -құралы.
Мен параболаны Гаусспен салыстыру үшін жасаған Geogebra диаграммасын мына сілтемеден табуға болады.
Бұл нұсқаулық ұзақ, себебі бұл демонстрация, бірақ егер сізде жарық диодты жарық ағынымен немесе Гауссиан қисықтары сәйкес келетін басқа құбылыспен байланысты мәселені тез арада шешуге тура келсе, онда сіз қадамда бекітілген электрондық кестеге өтіңіз. Бұл нұсқаулықтың 5 -і, бұл сіздің өміріңізді жеңілдетеді және сіз үшін барлық есептеулерді автоматты түрде жасайды.
Сізге қолданбалы математика ұнайды деп үміттенемін, себебі бұл нұсқаулық туралы.
1 -қадам: Монохроматты жарықдиодтан шығатын жарықты түсіну


Бұл талдауда мен спектрлік диаграммадан (бірінші суреттен) анық көріп тұрғандай, түрлі -түсті жарық диодтарының сериясын қарастырамын, олардың спектрлік қуатының таралуы орташа мәнінің -33 және +33нм -де х осіне айналатын Гауссқа ұқсайды. әдетте бұл ерекшелікті береді). Алайда, бұл диаграмманың көрінісі бір қуат блогындағы барлық спектрлерді қалыпқа келтіретінін ескеріңіз, бірақ жарық диодты шамалардың қуаты әр түрлі болады, олар қаншалықты тиімді өндірілгеніне және оларға қанша электр тогы (мА) береді.
Көріп отырғаныңыздай, кейде екі жарық диодты жарық ағыны спектрде сәйкес келеді. Айталық, мен бұл қисықтардың қабаттасатын ауданын оңай есептегім келеді, себебі бұл аймақта екі есе көп қуат болады және менде люменде (лм) қанша қуат бар екенін білгім келеді, олай емес біз бұл нұсқаулықта жауап беруге тырысатын қарапайым тапсырма. Мәселе туындады, себебі мен эксперименттік шамды құрған кезде көк және жасыл спектрдің қаншалықты сәйкес келетінін білгім келді.
Біз тек спектрдің тар бөлігінде шығатын монохроматты жарықдиодты шамдарға назар аударамыз. Диаграммада: КӨК КӨК, КӨК, ЖАСЫЛ, ОРАНЖЫЛ-ҚЫЗЫЛ, ҚЫЗЫЛ. (Мен құрастыратын нақты шам - RGB)
ФИЗИКА РЕТІНДЕ
Алдымен сәл артқа айналайық және физикаға сәл түсініктеме берейік.
Әрбір жарық диодының түсі бар, немесе ғылыми тұрғыдан алғанда біз оны анықтайтын толқын ұзындығы (λ) бар және нанометрлермен өлшенетін (nm) және λ = 1/f, мұндағы f - фотонның тербеліс жиілігі.
ҚЫЗЫЛ деп атайтынымыз - бұл 630нм тербелетін фотондар тобы (фотондар), бұл фотондар біздің көзімізге түседі, олар рецептор ретінде әрекет етеді, содан кейін сіздің миыңыз объектінің түсін ҚЫЗЫЛ өңдейді; немесе фотондар тікелей сіздің көзіңізге түсуі мүмкін, сонда сіз оларды шығаратын жарықдиодты қызыл түспен көресіз.
Біз жарық деп атайтынымыз 380нм мен 740нм арасындағы электромагниттік спектрдің аз ғана бөлігі екені анықталды; сондықтан жарық - электромагниттік толқын. Спектрдің бұл бөлігінің бір қызығы - бұл спектрдің дәл бөлігі судан оңай өтеді. Сіз қалай ойлайсыз? Біздің ежелгі ата -бабаларымыз алғашқы сорпадан шыққан, ол суда болады, ал суда тіршілік иелері бірінші болып күрделене бастайды. Мен сізге жарықтың не екенін жақсырақ түсіну үшін, мен қосқан Курцгесагтың бейнесін көруді ұсынамын.
Жарықдиодты жарық шығарады, бұл белгілі бір толқын ұзындығында (нм) радиометриялық қуаттың (мВт) белгілі бір саны.
Әдетте, біз көрінетін жарықпен жұмыс істегенде, біз радиометриялық қуат (мВт) туралы айтпаймыз, бірақ адам көзінің көрінетін жарығына жауап беретін өлшеу бірлігі болып табылатын жарық ағыны (лм) туралы айтамыз. кандела өлшем бірлігі, және ол люмен (лм) өлшенеді. Бұл презентацияда біз жарықдиодты шамдар шығаратын люмендерді қарастырамыз, бірақ бәрі де мВт -қа дәл сәйкесінше қолданылады.
Кез келген жарықдиодты деректер кестесінде өндіруші сізге келесі ақпаратты береді:
Мысалы, осы деректер кестесінен сіз екеуін де 100 мА қуаттандыратын болсаңыз, сізде бар екенін көресіз:
КӨК - 480нм және 11лм жарық ағыны;
GREEN - 530нм және 35лм жарық ағыны.
Бұл Гаусс көгілдір қисығы биік болады, ол енін өзгертпестен жоғарылайды және көк сызықпен бөлінген бөлігінің айналасында тербеліс болады дегенді білдіреді. Бұл жұмыста мен спектрдің сол бөлігінде шығарылатын қуатты ғана емес, жарық диодты шығаратын максималды қуатты білдіретін Гаусс биіктігін қалай есептеу керектігін түсіндіремін, өкінішке орай, бұл мән төмен болады. Сонымен қатар, мен спектрде «көрші» светодиодтармен жұмыс жасау кезінде жарық ағынының қаншалықты қабаттасатынын түсіну үшін екі жарық диодының бір -біріне сәйкес келетін бөлігін жақындатуға тырысамын.
Жарықдиодты ағынды өлшеу - бұл өте күрделі мәселе, егер сіз көбірек білгіңіз келсе, мен осрамның егжей -тегжейлі құжатын жүктедім, онда ол қалай жасалатынын түсіндіреді.
2 -қадам: Параболамен таныстыру


Мен парабола дегеніміз не, ол мектепте кеңінен зерттелгендіктен егжей -тегжейлі айтпаймын.
Парабола теңдеуін келесі түрде жазуға болады:
y = ax^2+bx+c
ARCHIMEDES бізге көмектеседі
Мен Архимедтің маңызды геометриялық теоремасының астын сызғым келеді. Теоремада айтылғандай, тіктөртбұрышпен шектелген параболаның ауданы тіктөртбұрыштың 2/3 бөлігіне тең. Параболасы бар бірінші суретте көгілдір аймақ 2/3, ал қызғылт аймақтар тіктөртбұрыш ауданының 1/3 бөлігін құрайтынын көруге болады.
Біз параболаның үш нүктесін біле отырып, оның теңдеуін есептей аламыз. Біздің жағдайда біз шыңды есептейміз және біз x осімен қиылыстарды білеміз. Мысалы:
Көгілдір жарық диоды шыңы (480,?) Шыңының Y шамасы толқын ұзындығында шығарылатын жарық қуатына тең. Оны есептеу үшін біз Гаусс ауданы (светодиоды шығаратын нақты ағын) мен параболаның арасында болатын қатынасты қолданамыз және сол параболаны қамтитын төртбұрыштың биіктігін білу үшін Архимед теоремасын қолданамыз.
x1 (447, 0)
x2 (513, 0)
ПАРАБОЛДЫҚ МОДЕЛЬ
Мен жүктеген суретке қарап, сіз параболалармен әр түрлі жарық диодты жарық ағындарын бейнелейтін күрделі модельді көре аласыз, бірақ біз олардың бейнеленуі Гауссқа ұқсас емес екенін білеміз.
Алайда, параболалар көмегімен математикалық формулаларды қолдана отырып, біз бірнеше параболалардың барлық қиылысу нүктелерін тауып, қиылысатын аудандарды есептей аламыз.
5 -қадамда мен электронды кестені тіркедім, онда мен монохроматты светодиодтардың барлық параболаларын және олардың қиылысатын аудандарын есептеу үшін барлық формулаларды қойдым.
Әдетте, Гаусс жарық диодының негізі үлкен 66 нм, сондықтан егер біз толқынның басым ұзындығын білсек және жарық диодты сәулеленуді параболамен жақындатсақ, салыстырмалы параболаның axis+33 пен λ-33 аралығында х осін қиып өтетінін білеміз.
Бұл параболамен бірге жалпы жарық диодты шамды шығаратын модель. Бірақ егер біз дәл болғымыз келсе, бұл дұрыс емес екенін білеміз, бізді келесі қадамға жеткізетін Гаусс қисықтарын қолдану қажет болады.
3 -қадам: Гаусс қисығына кіріспе




Гаусс - бұл қисық, ол параболадан гөрі күрделірек естіледі. Оны Гаусс қателерді түсіндіру үшін ойлап тапты. Шындығында, бұл қисықтың құбылыстың ықтималдық бойынша таралуын көру өте пайдалы. Орташадан солға немесе оңға қарай жылжытатын болсақ, бізде белгілі бір құбылыс сирек кездеседі және соңғы суреттен көріп отырғаныңыздай, бұл қисық нақты өмірдегі оқиғалардың өте жақсы жақындауы.
Гаусс формуласы - бұл қорқынышты, сіз оны екінші сурет ретінде көресіз.
Гаусс қасиеттері:
- бұл орташа мәнге қатысты симметриялы құрмет;
- x = μ орташа арифметикалық мәнмен ғана емес, сонымен қатар медиана мен режиммен сәйкес келеді;
- ол әр жағынан x осінде асимптотикалық;
- xμ үшін төмендейді;
- оның x = μ-in екі бұрылу нүктесі бар;
- қисық астындағы аудан - 1 бірлік (кез келген х тексеретін ықтималдылықпен)
σ - стандартты ауытқу, сан үлкен болған сайын Гаусс негізі кеңірек болады (бірінші сурет). Егер мән 3σ бөлігінде болса, біз оның орташа мәннен алыстап кететінін білеміз және оның болу ықтималдығы аз.
Біздің жағдайда, светодиодтарда біз Гаусс аймағын білеміз, ол өндіруші деректер кестесінде берілген толқын ұзындығының шыңында берілген жарық ағыны (бұл орташа мән).
4 -қадам: Геогебра көмегімен демонстрация

Бұл бөлімде мен сізге геогебраны қалай қолдану керектігін айтамын, ол параболаның Гаусстан 2,19 есе көп екенін көрсетеді.
Алдымен сіз жүгірткі пәрменін нұқып, бірнеше айнымалы жасауыңыз керек:
Стандартты ауытқу σ = 0.1 (стандартты ауытқу Гаусс қисығының қаншалықты кең екенін анықтайды, мен шамалы мәнді қойдым, себебі мен жарық диодты спектрлік қуаттың таралуын модельдеуді тар еткім келді)
Орташа 0 -ге тең, сондықтан Гаусс у осіне салынған, онда жұмыс істеу оңай.
Функция бөлімін іске қосу үшін кіші толқын функциясын басыңыз; fx түймесін басу арқылы сіз Гаусс формуласын енгізе аласыз және экранда биік Гаусс қисығы пайда болатынын көресіз.
Графикалық түрде қисық x осінде қай жерде жинақталатынын көресіз, менің жағдайда X1 (-0.4; 0) және X2 (+0.4; 0) және шыңы V (0; 4).
Осы үш нүктеде параболаның теңдеуін табу үшін жеткілікті ақпарат бар. Егер сіз қолмен есептегіңіз келмесе, келесі қадамда осы веб -сайтты немесе электрондық кестені қолданыңыз.
Сіз тапқан парабола функциясын толтыру үшін (fx) функция пәрменін қолданыңыз:
y = -25x^2 +4
Енді параболада қанша гауссиялық бар екенін түсінуіміз керек.
Сіз функция пәрменін қолданып, Integral (немесе менің жағдайда итальяндық нұсқаны қолданған кезде) интегралды пәрменін енгізуіңіз керек. Анықталған интеграл - бұл x мәндерінің арасында анықталған функцияның ауданын есептеуге мүмкіндік беретін математикалық операция. Егер нақты интеграл не екенін есіңізде болмаса, мына жерден оқыңыз.
a = интегралды (f, -0.4, +0.4)
Бұл Геогебра формуласы f функциясының -0.4 пен +0.4 арасындағы анықталған интегралды шешеді, Гаусс. Біз Гаусспен айналысатын болсақ, оның ауданы 1 -ге тең.
Парабола үшін де осылай жасаңыз, сіз 2.13 сиқырлы нөмірін табасыз. Жарық диодты жарық ағынының барлық түрлендірулерін жасайтын негізгі нөмір.
5 -қадам: Светодиоды бар нақты өмір мысалы: ағын шыңы мен қабаттасатын ағындарды есептеу


Шыңдағы нұрлы ағын
Жарықдиодты ағынның таралуының Гаусс қисықтарының нақты биіктігін есептеу үшін, біз 2.19 түрлендіру коэффициентін таптық, бұл өте оңай.
Мысалға:
Көгілдір жарық диодында 11 лм жарық ағыны бар
- біз бұл ағынды Гаусс тілінен параболалық 11 x 2.19 = 24.09 түрлендіреміз
- біз 24.09 x 3/2 = 36.14 параболасы бар салыстырмалы тіктөртбұрыш ауданын есептеу үшін Архимед теоремасын қолданамыз
- біз деректер кестесінде берілген немесе деректер кестесіндегі диаграммада көрінетін BLUE жарықдиодты Гаусс негізіне бөлінетін төртбұрыштың биіктігін табамыз, әдетте шамамен 66 нм, бұл біздің күш 480нм шыңында: 36.14 / 66 = 0,55
ШЫҒЫМДЫ АҒЫМДЫҚ АУДАНДАРДЫ ШЕКТЕУ
Бір -біріне сәйкес келетін екі сәулеленуді есептеу үшін мен келесі екі светодиодты мысалмен түсіндіремін:
КӨК - 480нм және 11лм жарық ағыны
Біз Гаусс қисықтарының -33нм және +33нм -де жақындасатынын диаграммадан білеміз және көреміз, демек біз білеміз:
- КӨК х осін 447нм және 531нм қиып өтеді
- GREEN х осін 497нм және 563нм қиып өтеді
Біз екі қисықтың біріншісінің бір ұшы екіншісінің (531нм> 497нм) басталуынан кейін қиылысатынын анық көреміз, сондықтан бұл екі жарықдиодты жарық кейбір нүктелерде қабаттасады.
Біз алдымен парабола теңдеуін екеуіне де есептеуіміз керек. Қосылған электрондық кесте сізге есептеуге көмектесу үшін және осьтің қиылысатын нүктелері мен төбесін білетін екі параболаны анықтау үшін теңдеулер жүйесін шешуге арналған формулаларды енгізді:
КӨК парабола: y = -0.0004889636025x^2 + 0.4694050584x -112.1247327
Жасыл парабола: y = -0.001555793281x^2 + 1.680256743x - 451.9750618
екеуінде де> 0 және, сондықтан парабола дұрыс төңкерілген.
Бұл параболалардың дұрыс екенін дәлелдеу үшін парабола калькуляторының веб -сайтындағы шыңы калькуляторында a, b, c толтырыңыз.
Электрондық кестеде параболалар арасындағы қиылысу нүктелерін табуға және сол параболалардың қиылысатын аудандарын алу үшін анықталған интегралды есептеуге арналған барлық есептеулер жүргізілген.
Біздің жағдайда көк және жасыл жарық диодты спектрлерінің қиылысатын аймақтары 0,4247 құрайды.
Бізде қиылысатын параболалар болғаннан кейін біз 0.4694 Гаусс мультипликаторы үшін жаңадан құрылған қиылысатын аймақты көбейте аламыз және спектрдің сол бөлігінде светодиодтар қанша қуат шығаратынына өте жақын жуықтауды таба аламыз. Бұл бөлімде шығарылатын жалғыз жарықдиодты ағынды табу үшін 2 -ге бөліңіз.
6 -қадам: Эксперименталды лампаның монохроматикалық жарық диодтарын зерттеу енді аяқталды


Жақсы, бұл зерттеуді оқығаныңыз үшін көп рахмет. Сізге шамнан жарықтың қалай шығатынын терең түсіну пайдалы болады деп сенемін.
Мен монохроматты жарықдиодтардың үш түрінен жасалған арнайы шамның жарық диодтарының ағындарын зерттедім.
Бұл шамды шығаратын «ингредиенттер»:
- 3 жарық диоды бар
- 4 жарықдиодты жасыл
- 3 қызыл ҚЫЗЫЛ
- жарық диодты тізбек тармақтарындағы токты шектеу үшін 3 резистор
- 12 В 35 Вт қуат көзі
- бедерлі акрил қаптамасы
- OSRAM OT BLE DIM басқару (Bluetooth LED басқару блогы)
- алюминий радиаторы
- M5 қалың және жаңғақ және L жақшасы
Барлығын смартфоннан Casambi APP көмегімен басқарыңыз, әр жарықдиодты арнаны бөлек қосуға және өшіруге болады.
Шам жасау өте қарапайым:
- жарықдиодты радиаторға екі жақты таспамен бекітіңіз;
- барлық BLU жарық диодты резистормен дәйекті дәнекерлеңіз және схеманың әр тармағы үшін басқа түспен де солай істеңіз. Сіз таңдайтын светодиодтарға сәйкес (мен Lumileds светодиодын қолдандым) сізге резистордың мөлшерін светодиодқа қанша ток берілетініне және 12 вольтты қоректендірудің жалпы кернеуіне байланысты таңдау керек болады. Егер сіз мұны қалай жасау керектігін білмесеңіз, мен сізге светодиодтар сериясының ток күшін шектеу үшін резистордың өлшемін қалай анықтау керектігін оқуға кеңес беремін.
-сымдарды Osram OT BLE әр каналына қосыңыз: светодиодтар тармақтарының барлық негізгі позитивтері ортақ (+), ал тармақтардың үш негативі сәйкесінше -B (көк) -G (жасыл)) -R (қызыл).
- Osram OT BLE кірісіне қуат көзін қосыңыз.
Osram OT BLE -нің керемет жағы мынада: сіз сценарийлер жасай аласыз және жарықдиодты арналарды бағдарламалай аласыз, себебі сіз бейненің бірінші бөлімінде үш арнаны қараңғылатып жатқаныңызды, ал мен қолданатын бейненің екінші бөлігінде. алдын ала жасалған жарық сценарийлері.
ҚОРЫТЫНДЫ
Мен бұл шамдардың ағыны қалай таралатынын терең түсіну үшін математиканы кеңінен қолдандым.
Сіз бүгін пайдалы нәрсе білдіңіз деп үміттенемін және мен осы сияқты терең қолданбалы зерттеулердің нұсқауларын беруге тырысамын.
Зерттеу - бұл кілт!
Көріскенше!
Пьетро
Ұсынылған:
Жарық диодты текшені қалай жасауға болады - Жарық диодты текше 4x4x4: 3 қадам

Жарық диодты текшені қалай жасауға болады | 4x4x4 жарықдиодты текше: LED текшесін жарықдиодты экран деп санауға болады, онда қарапайым 5 мм жарық диодты сандық пиксель рөлін атқарады. Жарық диодты текше көру қабілеттілігі (POV) деп аталатын оптикалық құбылыс тұжырымдамасын қолдану арқылы суреттер мен өрнектер жасауға мүмкіндік береді. Сонымен
Жарық диодты жарық диодты жылдамдықты басқарудың және баламалы жыпылықтаудың үш әдісі: 3 қадам

Жарық диодты жарық диодты айналдыру жылдамдығының реттелуінің және баламалы жыпылықтаудың үш әдісі: Флэшерлік схема - бұл конденсатор әсер ететін светодиодты қосатын және өшіретін схема, мұнда мен сізге осы схеманы жасаудың үш түрлі әдісін көрсетемін. : 1. Транзисторлар 2. 555 Таймер IC3. Quartz CircuitLDR -ді сонымен қатар
Жарық диодты жолағы мен жарық диодты схемасы бар супер эффектілер: 11 қадам

Жарық диодты жолағы мен жарық диодты схемасы бар супер эффектілер: Сәлем досым, мен бүгін жарық диодты және жарықдиодты жарық диодтары бар супер эффект шамдарының тізбегін жасаймын
Қарапайым жарық диодты схемасы (жарық диодты қалай қолдануға болады): 4 қадам
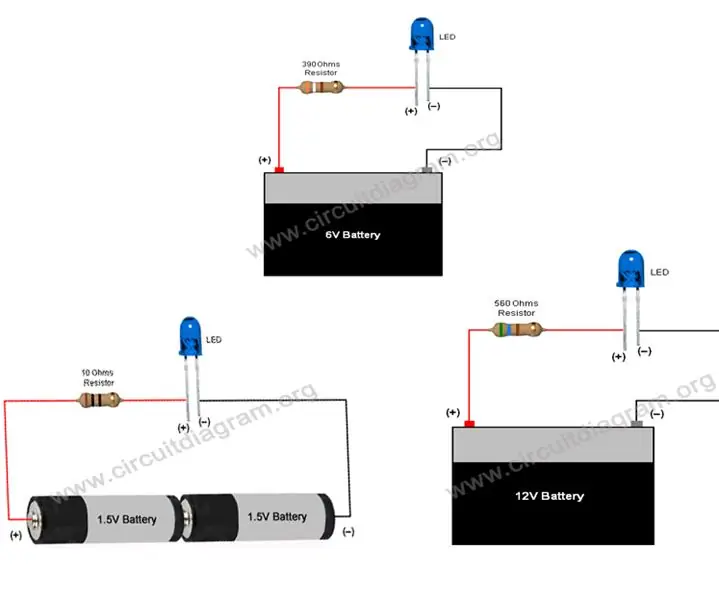
Қарапайым жарық диодты схемасы (жарықдиодты қалай қолдануға болады): Бұл нұсқаулық жарықдиодты қалай қолдануға және 3В, 6В, 9В & 12В. Жарық диоды электрониканың маңызды компоненті болып табылады, ол бірнеше индустрияда қолданылады
Түнгі жарық диодты түнгі жарық диодты шамы: 5 қадам

Түнгі жарық диодты түнгі жарық шамы / шамы: Біріншіден, бұл Sunbanks -тің шағын бос жарықдиодты шамының әсерінен болғанын айтуым керек. Жарықтандырғышты үстелден алшақ ұстау үшін, біро қолданудың орнына, мен базадан жарық түсіретін айқын перспективаны қолдандым. Бұл шағын жоба - бұл прототип
